1. Problems
CNNs have achieved many milestones in Computer Vision. They have been trained hierarchically with the concepts of learning low/mid/high-level features, the levels can be enriched by the number of stacked layers. According to He et al. (2015), the depth of the networks is crucially important to their accuracy, and the ImageNet winners only trained networks within 16 to 30 layers to achieve the highest performance.
Evidence shows that the best ImageNet models using convolutional and fully-connected layers typically contain between 16 and 30 layers.
But through several experiments, He et al. encountered the degradation of accuracy when training networks having a higher number of layers (image below). Unexpectedly, it turns out that the problem is not caused by vanishing gradient nor overfitting. Because the authors claimed that he used Batch Normalization against vanishing gradient, and the graphs also show that this is not the case of overfitting. Just adding more layers to suitably leads to higher training error.
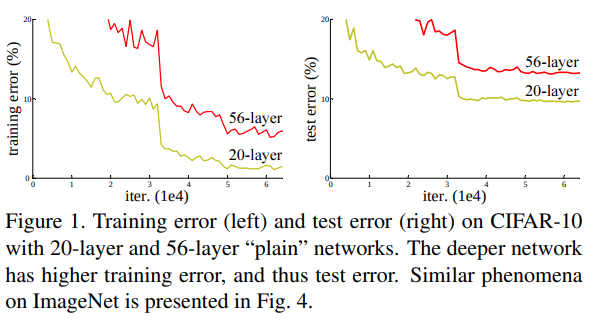
From Residual Neural Network paper
So how can we train the very deep networks to obtain state-of-the-art performance? That is why Residual Block and Residual Neural Network were designed to alleviate this problem.
2. Approach
Residual Block
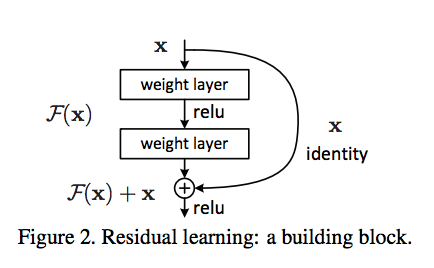
From Residual Neural Network paper
By understand this picture, you can understand how Residual Block works. There are some important modifications from the traditional design, they are Skip Connection and Identity Mapping. **Below is the formula for the diagram:
\[y = \underbrace{F(x)}_\text{Residual} + \underbrace{x}_\text{Identity}\]The above picture implies that apart from the output $F(x)$ by forwarding the input through the stacked layers, the block uses Skip Connection to pass a cloned version of $x$ to the end of the operation, then it uses Identity Mapping to combines $F(x)$ and $x$ together. In addition, **Identity Mapping does not have any parameters, so its contribution to model complexity is zero. In fact, according to He et al (2015):
We hypothesize that it is easier to optimize the residual mapping than to optimize the original, unreferenced mapping.
and
To the extreme, if an identity mapping were optimal, it would be easier to push the residual to zero than to fit an identity mapping by a stack of nonlinear layers.
⇒ In the end, in the case we have no ideas which layers are ineffective for the whole network, it can “push the residual to zero” (He et al., 2015, para. x). Besides, we only need to optimize $F(x)$ in backward propagation.
Multiple layers skipping
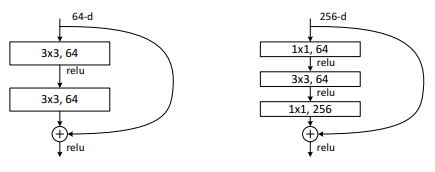
Note: Residual mapping is combining $F(x)$ with $x$
Problem: Sometimes $x$ and $F(x)$ do not share the same dimension or channels
⇒ Use 1 x 1 convolution with a new stride or new channel respectively to map $F(x)$
Residual Neural Network
Not just one layer, we can even skip multiple layers. For example, in the paper, the author skipped 2 convolutional layers in each residual block for ResNet-34.
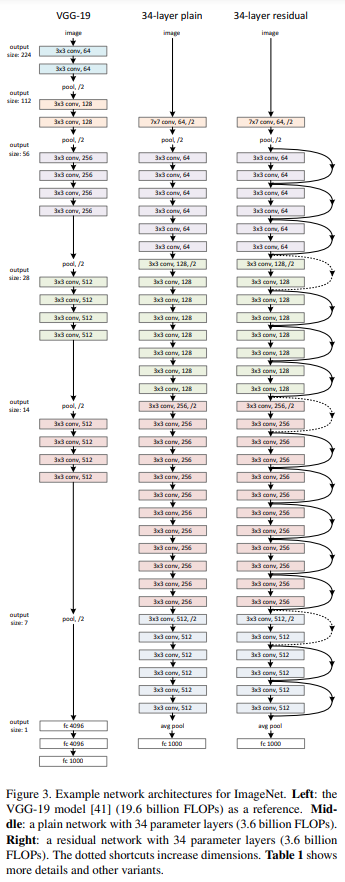
3. Code
Example code in PyTorch (from Dive into Deep Learning book):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from d2l import torch as d2l
import torch
from torch import nn
from torch.nn import functional as F
class Residual(nn.Module): #@save
"""The Residual block of ResNet."""
def __init__(self, input_channels, num_channels,
use_1x1conv=False, strides=1):
super().__init__()
self.conv1 = nn.Conv2d(input_channels, num_channels,
kernel_size=3, padding=1, stride=strides)
self.conv2 = nn.Conv2d(num_channels, num_channels,
kernel_size=3, padding=1)
if use_1x1conv:
self.conv3 = nn.Conv2d(input_channels, num_channels,
kernel_size=1, stride=strides)
else:
self.conv3 = None
self.bn1 = nn.BatchNorm2d(num_channels)
self.bn2 = nn.BatchNorm2d(num_channels)
self.relu = nn.ReLU(inplace=True)
def forward(self, X):
Y = F.relu(self.bn1(self.conv1(X)))
Y = self.bn2(self.conv2(Y))
if self.conv3:
X = self.conv3(X)
Y += X
return F.relu(Y)